Advanced Topics
Analemma and the Equation of Time
The analemma is the shape created by plotting the position of the Sun in the sky at the same civil time each day over the course of a year. The shape resembles a figure-eight and is a result of the tilt of the Earth’s axis and its elliptical orbit around the Sun.
The northernmost and southernmost points of the analemma are the solstices. Deviation from the arc joining these points is due to the difference between the true Sun and the mean Sun.
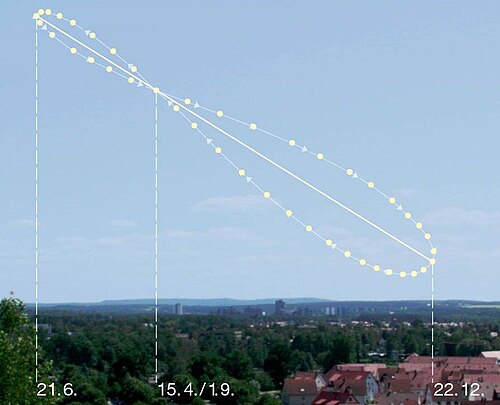
If the axial tilt is zero, the analemma would become an arc of a great circle. If the eccentricity of the orbit is zero, it will become a perfect figure-eight. If both are zero, the analemma will be a single point.
The following requires knowledge of Kepler’s laws and orbital anomalies, covered in chapter 3.2.
When viewed from different locations and at different times of the day, the position and orientation of the analemma change; however, the shape remains the same. Thus, without loss of generality, assume the observer is at the North Pole, and the Sun’s position is measured at noon. The altitude of the Sun will just be its declination , and its azimuth will be the difference in the right ascension of the Sun and the Mean Sun. Since the Mean Sun moves at a constant rate, its right ascension is just its mean anomaly . Let the ecliptic longitude of the Sun be , and its true anomaly be . These two are related by
where is the true anomaly of the vernal equinox. The true anomaly of the Earth is related to the mean anomaly of the Mean Sun by
where is the eccentricity of the orbit. This relation can be derived using Kepler’s second law, and the fact that the Mean Sun starts off from the vernal equinox instead of perihelion.
Using conversion identities (1.2.10), we can get the declination and right ascension of the Sun in terms of the ecliptic longitude:
Since the time period of the Sun and Mean Sun is the same, their mean anomaly too is the same. Thus, the altitude and azimuth of the Sun are
From this, we can conclude that the altitude difference between the lowest and highest points of the analemma is equal to twice the axial tilt of the Earth, . Closely examining the azimuth, we see that it is the difference between the right ascension of the Sun and the mean anomaly of the Mean Sun, which is just the equation of time . Equation (1.6.3) can be solved numerically to get the equation of time as a function of the mean anomaly , and also the shape of the analemma.
You can explore the analemma using all these interactive demos.
A detailed explanation of the equation of time is available at the wikipedia page. The analemma is not just observed for the Sun, but also for other celestial bodies like the Moon and planets. The analemma of the Moon, called the lunar analemma, looks just like that of the Sun, but is more elongated due to the higher eccentricity of the Moon’s orbit.
A few values of the equation of time are tabulated below (at epoch J2000):
| Point | Value | Date |
|---|---|---|
| minimum | 11 February | |
| zero | 15 April | |
| maximum | 14 May | |
| zero | 13 June | |
| minimum | 26 July | |
| zero | 1 September | |
| maximum | 3 November | |
| zero | 25 December |
Path of a Stick’s Shadow
Consider the path the shadow of a vertical stick traces out during a day, as the Sun moves across the sky. The shape traced out by the shadow is a conic section—an ellipse, parabola, or hyperbola—depending on the position of the Sun relative to the observer.
Let the latitude of the observer be and the declination of the Sun be . The length of the shadow of a unit length stick when the altitude of the Sun is is
We set up our coordinate system with the stick at the origin, the -axis pointing east, and the -axis pointing north. The angle the shadow makes with the north is just the azimuth of the Sun, . Thus,
Using transformation formulae, we get
Substituting these into the equations for and , we get
Eliminating the hour angle , we get
which is the equation of a conic section. The type of conic section depends on the values of and .
- Circle: , or when the observer is at pole
- Line: , or when sun is on the celestial equator
- Point: , or when the sun (hypothetically) is at the pole
- Ellipse: , or when the sun is circumpolar
- Parabola: , or when the sun just grazes the horizon at midnight
- Hyperbola: , or when the sun is not circumpolar
If , the Sun passes through the zenith at noon, and there is no shadow.