Magnitude Systems
Magnitude is a measure of the brightness of a star, astronomical object, or other celestial objects like artificial satellites. We would like to be able to communicate and express how bright an object is. For this, one could use the luminosity of the object or the flux received from that object. However, these numbers can get very large or very small. As a result, a magnitude scale is used.
Magnitudes are denoted by the unit ‘mag’, or with a superscript , although they have no dimensions. The scale is reverse logarithmic: the brighter an object is, the lower its magnitude number. A difference of 1.0 mag in magnitude corresponds to a brightness ratio of , or about 2.512. For example, a magnitude 2.0 star is 2.512 times brighter than a magnitude 3.0 star, 6.31 times brighter than a magnitude 4.0 star, and 100 times brighter than a magnitude 7.0 star.
Apparent magnitude is a measure of the brightness of an object as seen from Earth. It is related to how much flux is received from that object by the observer. It is usually denoted by .
Absolute magnitude, on the other hand, is a measure of the intrinsic brightness of an object, defined as the apparent magnitude it would have if it were located at a distance of 10 parsecs from the observer, without any extinction. The absolute magnitude of a star is directly related to its luminosity. It is usually denoted by .
The Greek astronomer Hipparchus produced a catalogue which noted the apparent brightness of stars in the second century BCE. In the second century CE, the Alexandrian astronomer Ptolemy classified stars on a six-point scale, and originated the term magnitude. To the unaided eye, a more prominent star such as Sirius or Arcturus appears larger than a less prominent star such as Mizar, which in turn appears larger than a truly faint star such as Alcor.
After several centuries of progress, in 1856 Norman Pogson, an English astronomer, proposed the modern logarithmic scale for magnitudes. This is the scale we use today.
Pogson’s Equation
The dimmer an object appears, the higher the numerical value given to its magnitude, with a difference of 5 magnitudes corresponding to a brightness factor of exactly 100. Let a flux value of correspond to a magnitude of . Then, the magnitude corresponding to an object having a flux of is given by Pogson’s equation, which reads
or equivalently,
where the base of the logarithm is 10.
Consider an object with luminosity , distance , apparent magnitude , and absolute magnitude . The flux received from the object at Earth is . The flux at from the object is . Ignoring extinction, we get
Hence we get that
If is measured in parsecs,
The distance modulus is defined as .
The difference in absolute magnitudes of two objects gives the ratio of their luminosities. If and are the absolute magnitudes of two objects, then
where and are the luminosities of the two objects.
If the two objects have radii and , and temperatures and , then we can find luminosity using the Stefan-Boltzmann law
From this we get
Using Pogson’s equation,
The light which we see coming from a double is the sum of the light from both components. Let be the flux which corresponds to a magnitude of 0. Let and be the luminosities of Albireo A and B, respectively. The total luminosity of the system is thus .
The luminosity of Albireo B can be found using
The total luminosity of the system can be found using
Hence the luminosity of Albireo A is
The apparent magnitude of Albireo A is given by Pogson’s equation as
Therefore we get that
Color Indices
Usually, filters are used to allow only certain wavelengths to enter the detector. This gives more information about the object than measuring the flux through all wavelengths at once. One such system of filters used commonly is the UBV system. It consists of three filters:
- The ultraviolet filter (U) is centered at 365 nm with an effective bandwidth of 66 nm
- The blue filter (B) is centered at 445 nm with an effective bandwidth of 94 nm
- The visual filter (V) is centered at 551 nm with an effective bandwidth of 88 nm
The apparent magnitudes measured through these filters are denoted by , and , or by , , and . The absolute magnitudes are denoted by , , and .
The color index is defined as the difference between the magnitudes measured through two different filters. For example, the color index is the difference between its and magnitudes
This gives the color of the star, which can be used to determine its temperature. The smaller the index, the bluer the star is, hence the hotter it is. Color indices of a star are independent of its distance.
The sensitivity function is defined as the fraction of a star’s flux detected by a filter at a given wavelength. It depends on the optics of the system, filter bandwidth and response of the photometer. For example, the apparent magnitude is given by
where is a constant. The apparent and magnitudes are defined similarly.
The color index is thus
where .
Bolometric Magnitude
Apparent magnitude is defined in a specific bandpass, such as the visual band, and depends on the sensitivity of the detectors used. The apparent magnitude of an object in the visual band or ‘V’ band is called the apparent visual magnitude of the object. The apparent bolometric magnitude is defined as the apparent magnitude of an object if all its radiation were collected and measured over all wavelengths. This would correspond to an ideal detector which is able to measure at all wavelengths with complete efficiency.
The absolute bolometric magnitude is defined as the absolute magnitude of an object if all its radiation were collected and measured over all wavelengths.
The bolometric correction is defined as the difference between the bolometric magnitude and the visual magnitude, given by
We also have that where and are the absolute bolometric and absolute visual magnitudes, respectively.
For the bolometric magnitude, the sensitivity function is unity everywhere: .
where is a constant.
By definition, bolometric correction is zero for F5 spectral type stars.
Find an expression for the bolometric correction, assuming the visual sensitivity function is given by
Where nm and nm.
Consider the zero point of both the visual and bolometric magnitudes to be the same, i.e. . Assume the emitting body emits like a perfect blackbody of temperature .
The visual magnitude is given by
The bolometric magnitude is given by
Thus the bolometric correction is given by
Since follows a blackbody spectrum, we can write
Where is the temperature of the object, is the radius of the object and is the distance to the object. Defining , and doing some algebra, we get that the expression for the bolometric correction simplifies to
where and . Numerical integration gives
The bolometric correction of the sun, which too has a temperature of about , is about . This large difference is due to the assumptions we made: Sun does not emit like a perfect blackbody, the zero points of the visual and bolometric magnitudes are not the same, and the sensitivity function is not a perfect rectangle, but rather shaped like a bell curve.
Lightcurve
A lightcurve is a plot of brightness versus time for a celestial object, such as a star.
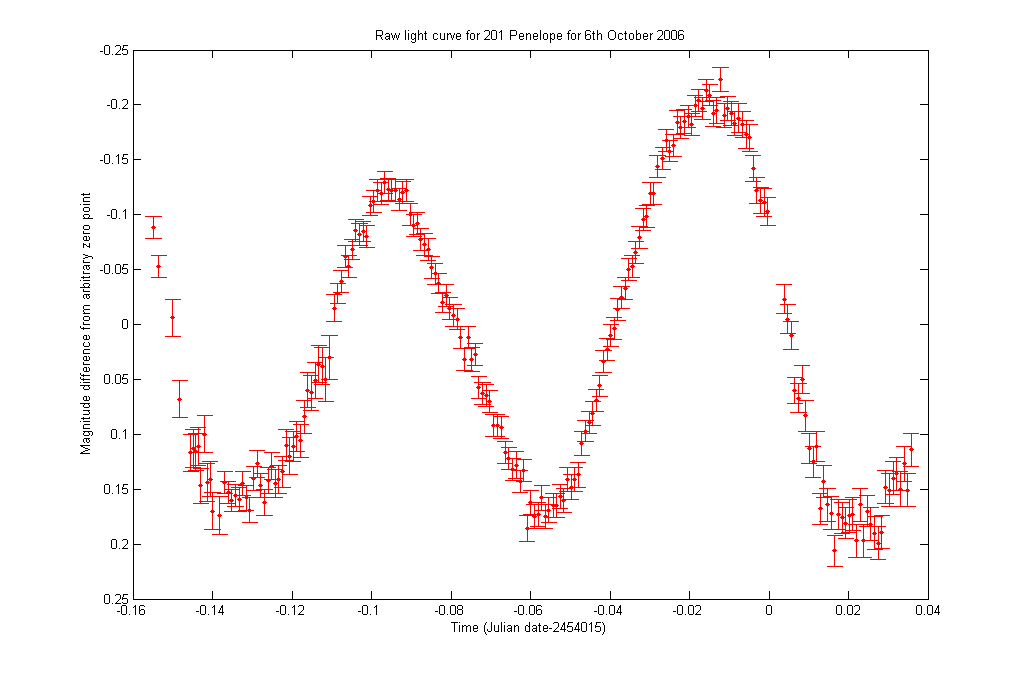
Tracking the lightcurve of a star can provide information about its properties. For example, periodic dips in brightness can indicate the presence of an exoplanet orbiting the star, as the planet passes in front of the star and blocks some of its light. Variations in brightness can also indicate changes in the star’s activity, such as flares or pulsations.
Extended Objects
For extended objects (which are not point-like), the total magnitude can be obtained by summing up the luminosity over the area of the object. The apparent magnitude of an extended object is defined as the magnitude of a point source that would produce the same total flux as the extended object.
Thus the total amount of light from a galaxy of would be the same as that from a star of . However, since the light from the galaxy is spread over a larger area, it will appear dimmer than the star.
For a comet, the total magnitude is the combined magnitude of the coma and the nucleus.
The surface brightness quantifies the apparent brightness of flux density per unit angular area of the spatially extended object. For an object with total magnitude extended over a visual area , its surface brightness is defined as
Surface brightness is measured in units of . This is a much more useful quantity when comparing brightness of extended objects.
Extinction
ISM
The space between the observer and the radiating source is often not empty and is filled with interstellar medium (ISM), which consists of gas and dust. As light passes through the ISM, some of it will be absorbed or scattered. This reduction of intensity of light in the direction of propagation is called extinction.
Suppose a star is radiating a flux into a solid angle . The flux will decrease with distance because of extinction
The opacity quantifies how effectively the medium can obscure radiation. For vacuum, . The dimensionless quantity , called the optical thickness or optical depth, is defined as
Here is the optical thickness between the source and the observer. This exponential decay is known as the Beer-Lambert law.
If is the flux density at the star’s surface and is the flux density at a distance ,
From this we get
where is the extinction in magnitudes due to the interstellar medium, as light goes from the star to the observer. gives the extinction in magnitudes per unit distance.
Extinction also causes reddening of light; blue light is scattered and absorbed more than red light, hence the color index increases.
where is the intrinsic color index of the star and the color excess is defined as .
Studies show that the ratio of the visual extinction to the color excess is almost constant for all stars
A star’s apparent magnitude in the V band is and absolute magnitude is equal to . Extinction of the interstellar medium per kpc is .
a) Find the distance to the star.
b) If the star’s observed color index is , find its intrinsic color.
c) If for the star, find its luminosity.
a) The distance modulus is given by
Where is measured in kpc, and . Substituting the values, we get
Solving it numerically, we get .
b) The intrinsic color index is given by
We can use the relation between and to find the color excess. The extinction in visual band is
Hence the color excess is
Thus the intrinsic color index of the star is
c) The bolometric magnitude of the star is
Comparing with the bolometric magnitude of the Sun gives the luminosity of the star
The absolute bolometric magnitude of the Sun is . Thus we get that the luminosity of the star is
Atmospheric Extinction
Earth’s atmosphere also causes extinction. The observed magnitude depends on the location of the observer and the zenith distance of the object. If the zenith distance is not too large, the atmosphere can be modelled by a plane layer of constant thickness. The airmass is defined as
This approximation holds good for .
The increase in magnitude is
where is the extinction coefficient, which depends on the wavelength of light and the atmospheric conditions. The extinction coefficient is defined as the increase in magnitude per unit airmass. is the true apparent magnitude, devoid of extinction effects.
Atmospheric extinction is usually negligible for objects at zenith, but can be significant for objects near the horizon.
Since depends on the wavelength, the color index is also affected by atmospheric extinction.
Problems
Using Pogson’s equation, we have
Substituting the values, we get
Hence the distance to Vega is approximately .
Note that since Vega is so close to us, the extinction effects are negligible, and we can ignore them in this case.
The apparent magnitudes of the Sun and the Moon are and , respectively. Thus the total extinction in the cloud must be . Since
where is the optical thickness of the fog, we can rearrange to get
Let the number density of stars be , and their absolute magnitude be . Let the apparent magnitude of the star at a distance pc from the observer be . and are related by the equation
Rearranging gives
All the stars brighter than magnitude will lies within pc distance to the observer. Thus the volume of the sphere upto radius is
The number of stars brighter than magnitude is given by
The number of stars brighter than magnitude is given by
The ratio of the two is given by
An old planetary nebula, with a white dwarf (WD) in its center, is located 50 pc away from Earth. Exactly in the same direction, but behind the nebula, lies another WD, identical to the frist, but located at 150 pc from the Earth. Consider that the two WDs have absolute bolometric magnitude +14.2 and intrinsic color indexes and . Extinction occurs in the interstellar medium and in the planetary nebula.
When we measure the color indices for the closer WD (the one who lies at the center of the nebula), we find the values and . In this part of the Galaxy, the interstellar extinction rates are 1.50, 1.23 and 1.00 magnitudes per kiloparsec for the filters U, B and V, respectively. Calculate the color indices as they would be measured for the second star.
Let , , be the intrinsic absolute magnitudes of the white dwarf. Let , , be the interstellar extinction coefficients per kpc. Let , , be the total extinction for the planetary nebula around the first WD, for light travelling from the centre of the nebula to the edge.
For the closer WD,
Similarily,
For second white dwarf, the extinction in planetary nebula will be doubled as extinction the light from this pulsar has to cross the entire diameter of the nebula. Overall distance of this pulsar is 3 times larger.
A UBV photometric observation of a star gives , , and . Based on the spectral class, one gets the intrinsic colour . If the star is known to have radius of , absolute bolometric magnitude of , and bolometric correction (BC) of , determine:
a) the intrinsic magnitudes U, B, and V of the star
b) the effective temperature of the star
c) the distance to the star
Take the ratio of total to selective extinction and the colour excess in to be about 72% of the colour excess in .
a) Let intrinsic magnitudes of the star be , , and respectively.
Since ,
Using the relation , we get
The intrinsic and color can be found using
b) Comparing the star’s bolometric magnitude to that of the Sun,
Substituting the values (), we get
c) The absolute visual magnitude can be found using the bolometric correction
Hence the distance can be found with (intrinsic apparent magnitude)
As the pulsar rotates, its beam sweeps out a conical surface. The solid angle into which radiation is emitted (by both poles) in one rotation is
To detect the pulsar, Earth must lie inside this solid angle. Hence the probability is
The pulsar emits radiation into a cone having solid angle
Thus the flux recieved on Earth is
Comparing the flux with the solar flux gives the apparent magnitude of the pulsar
A star has an apparent magnitude in the U-band. The U-band filter is ideal, i.e., it has perfect (100%) transmission within the band and is completely opaque (0% transmission) outside the band. The filter is centered at 360 nm, and has a width of 80 nm. It is assumed that the star also has a flat energy spectrum with respect to frequency. The conversion between magnitude, , in any band and flux density, , of a star in Jansky is given by
a) Approximately how many U-band photons, , from this star will be incident normally on a area at the top of the Earth’s atmosphere every second?
This star is being observed in the U-band using a ground based telescope, whose primary mirror has a diameter of . Atmospheric extinction in U-band during the observation is 50%. You may assume that the seeing is diffraction limited. Average surface brightness of night sky in U-band was measured to be .
b) What is the ratio, , of number of photons received per second from the star to that received from the sky, when measured over a circular aperture of diameter ?
c) In practice, only 20% of U-band photons falling on the primary mirror are detected. How many photons, , from the star are detected per second?
a) The U-band is defined as () nm. Thus, the minimum, maximum and average frequencies of the band are
Now, , where and .
b) Let us call sky flux per square arcsec as and total sky flux for the given aperture as . Let total star flux be .
Using the formula for surface brightness, we get that the magnitude corresponding to this flux is
As extinction is 50%,
c) Equating the number of photons,
The star -Doradus is a Cepheid variable star with a pulsation period of 9.84 days. We make a simplifying assumption that the star is brightest when it is most contracted (radius being ) and it is faintest when it is most expanded (radius being ). For simplicity, assume that the star maintains its spherical shape and behaves as a perfect black body at every instant during the entire cycle. The bolometric magnitude of the star varies from to . From Doppler measurements, we know that during pulsation the stellar surface expands or contracts at an average radial speed of . Over the period of pulsation, the peak of thermal radiation (intrinsic) of the star varies from 531.0 nm to 649.1 nm.
a) Find the ratio of radii of the star in its most contracted and most expanded states ().
b) Find the radii of the star (in metres) in its most contracted and most expanded states ( and ).
c) Calculate the flux of the star, , when it is in its most expanded state.
d) Find the distance to the star, , in parsecs.
a) The ratio of the fluxes is
The flux is given by , if the star is at a distance from the observer.
Hence we get that
Using Wien’s displacement law, .
b) The radial velocity causes the change in radius of the star
c) To get the absolute value of flux () we must compare it with observed flux of the Sun.
d) The temperature of the star when it is fully expanded is
The distance can be found using the observed flux
Assuming the star to be a blackbody, the spectral flux density in the Wien approximation of the star is propotional to
The color index is defined as
Using the given wavelengths and , the term . Assuming standard zero-point calibration, we get the approximate relation: